Simple Random Walks

It was noted early on that the markets resemble to random processes. Thus we could try to simulate a market with an appropriate random processes.

A simple such random process is the Random Walk, for which we take equal size "steps" either increasing, or decreasing a security's value in random (for example with a 50% probability for either way). After several iterations we could get the probability distribution of the price of the security over time.

To have a better idea of how random walks look like, a simple Random Walk model applet is available [here].

Hurst Random Walks

An improvement of the random walk is the biased (hurst) random walk. Specifically, we change "step" direction with either a lower (in our case) or a higher probability. This way we can simulate the market even better, as it is more likely for a trend to continue for the next day.

For our random walks, a hurst exponent of 0.57 is used. This means that for each step of the simulation we change step direction with a 43% probability. The use of this particular value is a result of a CSE691 project on random walks by G. Longo, which can be found [here].

Random Walk Graphs

The "average" (predicted price distribution) graphs provides the probability distribution for a stock price until the end of the year, and it gives you the current percentile. For example, if a stock reports a percentile of 70% then it closed better than 70% of our random walks, indicating rather good performance. Here is the detailed key for the predicted price distribution graphs:

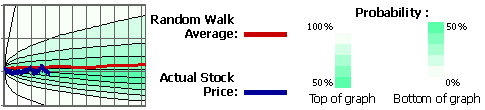
The "min / max" (High to Date and Low to Date) graph shows the probability for a stock to either rise or to have risen to a specific high price, or to have dropped to a low price. For example, if your stock price corresponds to a max (blue) percentile of 60%, then for 60% of the random walks, the model had not reached the current price at any date up to today. Here is the detailed key for the High to Date / Low to Date graphs:

Note that the average historic volatility (Parkinson High-Low) is calculated using the previous year's quotes. A standard drift of 7% is always applied to the calculation, which is the growth we get if we see the stock market at a historic perspective (i.e. Dow Jones Industrial index for over half a century).